30.114 Advanced Feedback and Control
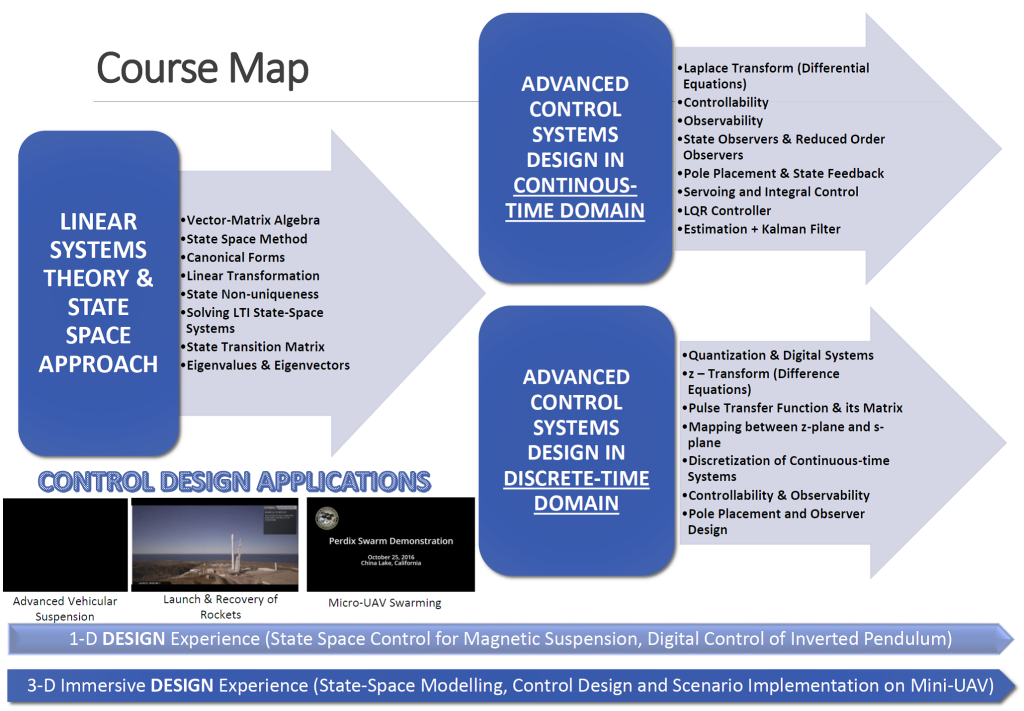
Extending feedback control theory and applications (from 30.101 Systems & Control) to include multi-input & multi-output and discrete-time systems. Mathematical modeling and analysis of discrete time systems in various disciplines using state-space, pulse transfer function and z-transform. Relating controllability and observability and their canonical forms to synthesize and design advanced continuous and discrete-time controllers. Introduction of pole-placement based controller design and formulation of state observers.
Goal
The goal of this class is to build on understanding of linear time-invariant state space systems to synthesize and evaluate advanced feedback controllers as well as digital implementation of such controllers. It has wide applications including, mechatronics, robotics, automation, space technology, transportation & aviation, medical systems, financial markets and energy management.
Learning objectives
- Represent physical systems in continuous state-space canonical forms and solve the linear time-invariant (LTI) state equation.
- Assess the controllability and observability of LTI state-space continuous-time and discrete-time systems for stability analysis, design of controllers and regulators with specific dynamic performances.
- Extend modelling principles to describe discrete-time systems and represent them using pulse transfer functions and state-space.
- Analyze and synthesize discrete time control systems using the z transform and root locus.
- Convert a continuous time system to a discrete-time system and vice-versa.
Measurable outcomes
- Given a physical system, conceive a set differential equations and difference equations describing continuous and discrete-time model of the system and representing it state-space. [LO1, LO3]
- Describe the notion of controllability and observability for both continuous and discrete-time systems and design full and reduced-order state observers and state feedback and integral controllers [LO2].
- Apply Eigenvalue analysis to determine poles and subsequent stability of state-space system. [LO2]
- Based on a performance specification, design a suitable digital compensator for a discrete-time system using z-transform and on the z-plane using root-locus analysis. [LO2]
- Model and represent discrete time signals and systems using the z Transform and solve LTI difference equation and the systems that these equations describe using the inverse z transform and the z plane. [LO4]
- With a system described in a continuous-time representation, express the corresponding system in a discrete-time representation and be able to map between the s-plane of continuous systems to z-plane of discrete-time systems. [LO5]
Pedagogy
Integrated and unified theoretical and practical approach in continuous-time and discrete-time control engineering and their applications. Embedded 1D, and 3D group and individual design activities.
Class structure:
- Monday (2.5 hr): Active Learning
- Tuesday (2.5 hr): Active Learning + Design Experience (1D/3D)
All handouts and supplements will be available on eDimension.
Software integration:
- MATLAB and Control System Toolbox
- LabVIEW and Control Design Toolkit plus Quanser QNETs
- C Programming and Ubuntu (Virtual Machine)
Grading
- Finals – 30%
- Mid-term – 25%
- 1D / 3D Design Experience – 20%
- In-class Assignments & Homework – 15%
- Instructor Prerogative (e.g. attendance) – 10%
Prerequisite
Policies
Late submissions will be penalized.
Text and references
Primary Texts
- Feedback Control of Dynamic Systems by Gene F. Franklin, J. David Powell, Abbas Emami-Naeini
- Modern Control Engineering by Katsuhiko Ogata
- Discrete-time Control Systems by Katsuhiko Ogata
Additional References:
- Digital Control of Dynamic Systems by Gene F. Franklin, J. David Powell, Michael Workman
- Linear Systems Theory by João P. Hespanha.
- Linear Systems by Thomas Kailath.
